18.아핀변환(Affine Transformation)

민돌이2 2022. 1. 20. 17:34

아핀변환은 선형변환에 이동이 결합된 것이다. 벡터에 대해서 다시 생각해보면 벡터는 크기와 방향만 갖고 있고, 이동에 대해서는 아무런 의미가 없다. 쉽게 말해서 벡터는 이동에 대해서는 불변이여야 하고, 이동은 점에만 적용되어야 한다.

동차좌표(homogeneous coordinate)를 이용하면 점과 벡터를 동일한 방식으로 다룰 수 있다. 동차좌푠느 3차원 벡터에 w성분을 추가한 4원소 형태이다. w의 값에 따라 점인지 벡터인지 결정된다.

1.벡터의 경우(x, y, z, 0)

2.점의 경우(x, y, z, 1)

즉, w = 0이면 벡터, w = 1이면 점으로 취급한다.

3차원 그래픽에 사용하는 변환들 중에는 선형변환으로 구현이 불가능한 것들이 있다. 이런 것들을 아핀변환을 사용하여 해결해야 할 때가 있다.

아핀변환은 선형변환에 이동 벡터를 더하여 사용한다.

위의 식을 행렬로 표기하면 아래와 같다.

A는 선형변환의 행렬 표현이다.

w = 1인 동차좌표를 도입하면 4 × 4 행렬을 아핀변환의 행렬 표현이라고 부른다.

주어진 인수를 그대로 선형변, 즉 I(u) = u를 항등변환(identity transformation)이라고 부른다. 이동 변환을 선형변환 부분이 하나의 단위행렬인 아핀변환이라고 정의할 수 있다.

위의 식을 보면 단위행렬인 I와 점 u를 곱해도 점 u가 나오므로 결론적으로 점 u를 b만큼 이동한다.

이동을 행렬로 표현하면 이동행렬이 된다. 이동 행렬은 아래와 같다.

동차인 4행 4열의 원소는 1이므로 점이고, 1행 1열, 2행 2열, 3행 3열의 원소 모두 1이므로 단위 행렬이고 이동하는 b는 4행에 위치한다.

이동행렬의 역은 아래와 같다.

이동을 담당하는 4행의 1~3열의 원소 즉, b들의 값에 음수만 취해주면 된다.

만일 이동을 담당하는 b = 0이면 아핀변환은 선형변환이 된다. 즉, b = 0 으로 만듬으로써 선형변환을 아핀변환으로 표현할 수 있다.

첫 번째 행렬은 비례행렬이고, 두 번째 행렬은 회전행렬임을 기억하자.

강체변환(rigid body transfromation)은 변환 시 물체의 형태가 그대로 유지되는 변환이다. 비유를 해보면, 마우스는 책상 위에 있고 마우스를 사용을 하면서 이동하고 회전할 것이다. 이 변환을 아핀변환으로 표현할 수 있다.

τ는 마우스의 회전을 나타내는 회전 변환이고 b는 마우스의 이동을 나타내는 이동 변환이다.

이를 동차좌표와 행렬로 표기하면 아래와 같다.

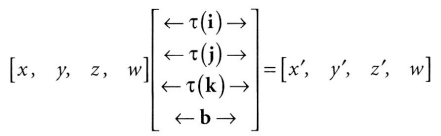
w = 0이라면 점이고, w = 1이라면 벡터임을 기억하자.

위의 행렬을 보고 기억해야 하는 것은 한 행렬에 회전과 이동을 동시에 담고 있다는 점이다.

회전을 담당하는 τ는 표준기저벡터 i, j, k만을 위한 τ(i), τ(j), τ(k)로 회전하고, 이동을 담당하는 벡터 b는 원점으로 부터의 변위를 나타내느 위치벡터이다.

x, y, z축 상에서 이동과 회전을 그림으로 본다면

위 그림에서 (a)에서 회전과 이동을 하면 (b)가 된다.

728x90