23.변환 요약

1. 비례, 회전 이동 변환 행렬은 아래와 같이 주어진다.
   

   

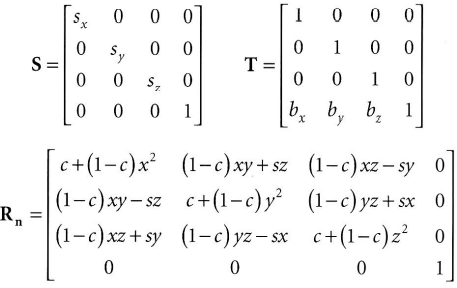
2. 변환은 4 × 4 행렬로 나타내고 점과 벡터는 1 × 4 동차좌표로 나타낸다. 점의 경우 넷째 성분을 w = 1로 설정하고 벡터의 경우에는 w = 0응로 설정한다. 점에 대해서는 이동변환이 적용되지만 벡터에 대해서는 적용되지 않는다.
3. 모든 행벡터가 단위길이이고 서로 직교인 행렬을 직교행렬이라고 한다. 직교행렬은 그 역이 전치와 같다는 성질을 갖고 있다. 따라서 역행렬을 쉽고 효율적으로 계산할 수 있다. 모든 회전행렬은 직교행렬이다.
4. 행렬 곱셈의 결합법칙 덕분에, 여러 개의 변환 행렬을 결합해서 그 행렬들을 차례로 적용했을 때와 같은 결과를 내는 하나의 변환 행렬을 만들 수 있다.
5. Q_B와 u_B, v_B w_B가 좌표계 A의 원점, x축, y축, z축의 좌표계 B 기준 좌표들이라고 할때, 어떤 벡터 또는 점 p의 좌표계 A 기준 좌표가 P_A = (x, y, z)라고 할 때, 그 벡터 또는 점의 좌표계 B기준 좌표는 다음과 같다.
   (a) 벡터(방향과 크기)의 경우 p_B = (x', y', z') = xu_B + yv_B + zw_B
   (b) 점(위치벡터)의 경우 p_B = (x', y', z') = Q_B + xu_B + yv_B + zw_B
6. 세 개의 좌표계 F, G, H가 있을 때, A가 F에서 G로의 좌표 변경 행렬이고 B가 G에서 H로의 좌표 변경 행렬이다. 이때 행렬 곱셈으로 얻은 행렬 C = AB를 F에서 직접 H로 가는 좌표 변경 행렬로 간주할 수 있다. 즉, 행렬ㅌ행렬 곱셈은 A의 효과와 B의 효과를 하나의 행렬로 결합한다. 따라서 p_F(AB) = p_H가 성립한다.
7. 만일 M이 좌표계 A의 좌표들을 좌표계 B의 좌표들로 사상하는 행렬이라면, 행렬 M^-1은 좌표계 B의 좌표들을 A의 좌표들로 사상하는 행렬이다.
8. 능동 변환들을 좌표 변경 변환으로 해석할 수 있고 그 역도 마찬가지이다. 여러 개의 좌표계들을 다루면서 물체 자체는 변경하지 않고 좌표계만 변경함으로써 물체의 좌표 표현이 바뀌게 하는 것이 더 직관적인 상황도 있고, 반대로 하나의 좌표계로 고정하고 그 좌표계 안에서 물체 자체를 변환하는 것이 더 직관적인 상황도 있다.