입력 조립기(IA) 단계에서 기본도형들을 조립한 후에는 정점들이 정점 셰이더 단계(vertex shader)로 입력된다. 화면에 그려질 모든 정점들은 정점 셰이더를 거쳐 간다. 정점 셰이더의 구체적인 내용은 프로그래머가 구현해서 GPU에 제출한다. 그 함수는 GPU에서 실행되기 때문에 아주 빠르다.
1.국소 공간(local space)과 세계 공간(world space)
책상 위에 핸드폰이 있다고 할 때, 국소 공간(local space)은 책상의 핸드폰의 좌표이고, 세계 공간(world space)은 방에서의 핸드폰의 좌표로 비유할 수 있다. 국소 공간은 세계 공간에 포함되는 포함관계와 비슷하다고 생각하면 된다.
국소 공간은 로컬 좌표라고 하고 세계 공간은 월드 좌표라고 한다.

위 그림에서 도형의 좌표계가 로컬 좌표계다.
로컬 좌표에서 월드 좌표로 변환하는 과정을 세계 변환(world transform)이라고 하고, 해당 변환 행렬을 세계 행렬(world matrix)이라고 한다.
한 물체에 대한 세계 행렬은 월드 좌표를 기준으로 한 로컬 좌표의 위치와 방향을 나타내는 행들로 이루어진 행렬이다.
Qw = (Qx, Qy, Qz, 1)과 uw = (ux, uy, uz, 0), vw = (vx, vy, vz, 0), ww = (wx, wy, wz, 0)이 월드 좌표를 기준으로 한 로컬 좌표의 원점, x축, y축, z축을 뜻하는 동차좌표들이라고 할 때, 로컬 좌표를 월드 좌표로 변환하는 좌표 변경 행렬은 아래와 같다.
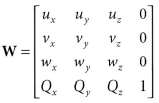
이런 세계 행렬을 만들기 위해서는 월드 좌표를 기준으로 한 로컬 좌표의 원점 및 축들의 좌표를 알아야 한다. 다른 방법으로 W = SRT 형태로 변환하는 것이다. 로컬 좌표를 월드 좌표로 변환할 때를 기준으로 S는 비례행렬, R은 회전행렬, T는 이동행렬이다.
2.시야공간
어떤 화면을 렌더링 한다는 것은 결국 가상의 카메라를 기준으로 바라보는 장면을 렌더링 한다는 것이다. 이 카메라에 로컬 좌표계를 부여한다고 하자. 이 좌표계를 시야 공간(view space)라고 하고, 시점 공간(eye space) 또는 카메라 공간(camera space)라고도 한다. 나는 주로 카메라 좌표라고 한다. 카메라는 이 공간의 원점에 놓고 카메라의 오른쪽 방향을 양의 x축, 위 방향을 양의 y축, 정면을 양의 z축으로 기준을 잡는다. 월드 좌표에서 카메라 좌표로의 좌표 변경 변환을 시야 변환(view transform)이라고 부르고, 해당 변환 행렬을 시야 행렬(view matrix)이라고 한다.
월드 좌표를 기준으로 한 로컬 좌표의 원좜과 x, y, z 축들을 나타내는 동차좌표들이 Qw = (Qx, Qy, Qz, 1)과 uw = (ux, uy, uz, 0), vw = (vx, vy, vz, 0), ww = (wx, wy, wz, 0)이라고 할 때, 카메라 좌표에서 월드 좌표로의 좌표 변경 변환 행렬은 아래와 같다.
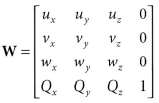
하지만 카메라는 화면을 렌더링할 시야를 담당할 뿐이다. 카메라 좌표에서 월드 좌표로의 세계 변환이 아니라 월드 좌표에서 카메라 좌표의 세계 변환이 필요하다. 즉, 위의 좌표 변경 변환 행렬의 역행렬이 필요하다. 진짜로 필요로 하는 역행렬은 아래와 같다.

시야 행렬을 구축하는 데 필요한 벡터들을 직접 구하는 방법은 카메라의 위치와 대상점, 월드 좌표의 상향 벡터만 있으면 구할 수 있다.
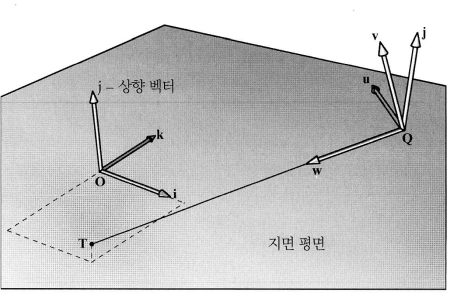
위 그림에서 Q는 카메라의 위치이고, T는 카메라가 바라보는 지점이다. j는 월드 좌표의 상향 벡터(up vector)이다.
카메라가 바라보는 정면은 z축이므로 w는 z축이다. 이 사실을 이용하여 w, u, v벡터 즉, 카메라의 x, y, z축을 구할 수 있다.

벡터 w는 벡터의 차를 이용하여 구하고, 벡터 u는 월드 좌표의 상향 벡터와 w의 외적을 이용하고, 벡터 v는 w와 u의 외적으로 구한다.
XNA Math 라이브러리는 시야 행렬을 계산하는 함수를 제공한다.
XMMATRIX XMMatrixLookAtLH(FXMVECTOR EyePosition, FXMVECTOR FocusPosition, FXMVECTOR UpDirection);
3.투영과 동차 절단 공간
카메라의 위치와 방향이 있고 카메라가 바라보는 공간 영역이 있따. 이 영역은 절두체(frustum)로 정의된다.

이 절두체안에 있는 물체나 공간들이 렌더링 되는 것이다. 즉, 절두체는 카메라로 보이는 공간 영역을 정의한다.
절두체 안에 있는 3차원 기하구조를 2차원 평면으로 투영(projection)하여 렌더링 한다. 3차원의 렌더링을 위해서는 이 투영이 반드시 평행선들이 하나의 소실점으로 수렴하는 방식이 되어야 한다. 소실점은 카메라의 위치가 된다.
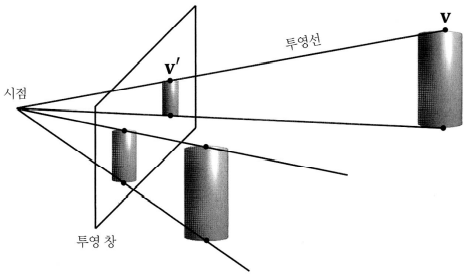
위 그림을 보면 시점으로 투영선이 모이면서 크기가 줄어드는 것을 알 수 있다. 멀리 있을 수록 크기는 더욱 줄어든다. 정점에서 시점으로의 직선을 정점의 투영선(line of projection)이라고 하고 이 방식을 원근투영(perspective projection)이라고 한다. 원근투영 변환은 하나의 3차원 정점 v와 v의 투영선이 투영 평면과 만나는 점 v'으로 변환하는 변환이다. 이 v'를 v의 투영이라고 부른다.
카메라와 거리가 멀다는 것은 깊이가 크다는 것이고, 깊이가 증가함에 따라 투영창에 투영된 결과의 크기가 줄어 든다는 것을 잊지 말자.
시야 공간에서 시점을 원점에 두고 양의 z축을 바라보는 시야 절두체를 다섯 가지 수량을 이용해서 정의할 수 있다.
- 원점과 가까운 평면 사이의 거리 n
- 원점과 먼 평면 사이의 거리 f
- 종횡비 r
- 수직 시야각 α
- 수평 시야각 β
시야 공간에서 가까운 평면과 먼 평면은 카메라 좌표의 xy 평면과 평행하다는 것은 머리속에 그릴 수 있어야 한다. 따라서 원점과 평면 사이의 거리인 n과 f는 z축 상의 거리일 뿐이다.
종횡비(aspect ratio)는 아래의 공식으로 정의된다.

w는 투영 창의 너비이고 h는 투영 창의 높이이다. 투영 창은 카메라가 바라본 장면이고, 그 장면을 화면에 렌더링하는 이미지이다. 결국 후면 버퍼에 사상되는 것으로, 투영 창의 너비와 높이의 비율은 후면 버퍼의 비율과 같게 만드는 것이 바람직하다.
수평 시야각은 시야각 알파와 종횡비 r로부터 구할 수 있다.
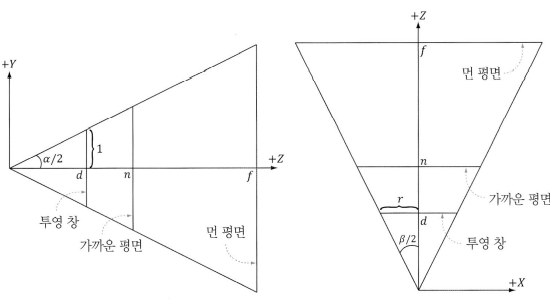
왼쪽 그림은 높이가 2라고 가정한 그림이다. 높이가 2일 때 다음과 같은 식을 정의할 수 있다.
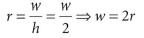
왼쪽 그림을 이용하여 투영 창의 거리 d를 구할 수 있다.
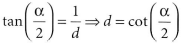
이제 수평 시야각 β를 유도할 수 있다.

절두체 안의 점 (x, y, z)가 있을 때, 투영 창에 투영한 점 (x', y', d)를 구하고자 한다.
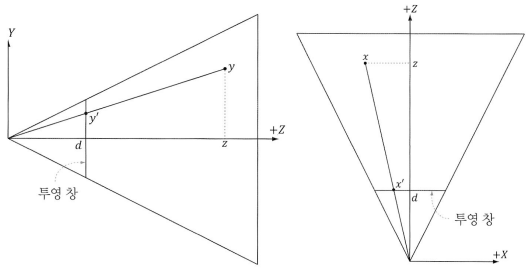
원본 평면인 z와 투영창의 평면인 d는 평행함으로 닮은꼴 삼각형의 원리를 적용할 수 있다.

투영창의 크기는 종횡비에 의존 하는데 이는 하드웨어가 투영 창의 크기에 관련한 연산들을 할 때마다 종횡비를 알아야 함을 의미한다. 하드웨어가 종횡비로부터 의존성을 없애려면 정규화(normalization)를 이용한다. 정규화란 [-r, r]을 [-1, 1]로 비례시키는 것이다. 정규화한 좌표를 정규화된 장치 좌표(normalized deice coordinates : NDC)라고 부른다.
투영 변환을 행렬로 표현하면 아래와 같다.
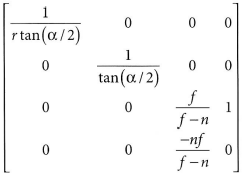
XNA Math 라이브러리는 원근투영 행렬을 구축해 주는 함수를 제공한다.
XMMATRIX XMMatrixPerspectiveFovLH(FLOAT FovAngleY, FLOAT AspectRatio, FLOAT NearZ, FLOAT FarZ);'서적 정리 > DirectX11을 이용한 3D 게임 프로그래밍 입문' 카테고리의 다른 글
| 39.래스터화기 단계(Rasterizer Stage : RS) (0) | 2022.01.25 |
|---|---|
| 38.절단(clipping) (0) | 2022.01.25 |
| 37.기하 셰이더(Geometry Shader : GS) 단계 (0) | 2022.01.25 |
| 36.테셀레이션(Tessellation) 단계 (0) | 2022.01.25 |
| 34.입력 조립기(Input Assembler : IA) 단계 (0) | 2022.01.23 |
| 33.렌더링 파이프라인의 개요 (0) | 2022.01.21 |
| 32.색상 표현의 기초 (0) | 2022.01.20 |
| 31.모형의 표현 (0) | 2022.01.20 |




댓글