1.정의
수학 함수 τ(v) = τ(x, y, z) = (x', y', z')라고 가정해보자. 이 함수는 3차원 벡터 하나를 받아서 3차원 벡터를 산출하는데 이런 경우에만, τ를 가르켜 선형변환이라고 부른다.

또한 τ가 선변현환이면 다음을 만족한다.

2.행렬 표현
벡터 u = (x, y, z)가 있다고 생각해보자. 벡터를 다르게 표현해본다면

i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1)이고 x, y, z는 스칼라 값인건 쉽게 이해할 수 있다. 또한 i, j, k는 각각 x, y, z축의 단위 벡터들이고 이들을 R3에 대한 표준기저벡터(standard basis vector)라고 부른다. 지수는 차원의 수를 나타내며 2차원 공간의 표준 기저벡터는 R2로 나타낸다.
이제 벡터에 대해 선형변환을 한다고 하면 위의 식은 아래의 식이 성립된다.

여기서 생각을 좀 더 해보면 벡터를 행렬로 표현할 수 있다.

여기서 τ(i) = (A11), A12), A13)), τ(j) = (A21), A22), A23)), τ(k) = (A31), A32), A33)이다. 이러한 행렬 A를 선형변환 τ의 행렬 표현이라고 한다.
3.비례(scaling)
비례는 물체의 크기를 바꾸는 효과를 나타낸다. 비례 변환은 아래와 같이 정의된다.

비례 변환에 의해 벡터는 현재 좌표계를 기준으로 하여 x축으로 sx단위, y축으로 sy단위, z축으로 sz단위 만큼 비례된다. 알아야 할 것이 비례 변환 또한 선형변환이다.

위의 식으로 비례 변환은 하나의 선형변환이고, 행렬 표현이 가능하다는 결론으로 도달할 수 있다.
s의 행렬을 비례행렬(scaling matrix)라고 부른다.

sx, sy, sz를 간단하게 s라고 치환했을 때 s > 1이라면 확대가 될 것이고, s < 1이라면 축소가 이뤄질 것이다.
4.회전(Rotate)
벡터 v를 축 n에 대해 각도 θ만큼 회전한다고 생각해보자. 벡터 v의 머리쪽에서 꼬리 쪽 방향으로 축 n을 바라보는 시점에서 시계방향으로 회전한다.
회전을 할 때 벡터 v를 두 벡터로 분해하고 생각해 보자.
1.축 n에 평행한 벡터 projn(v)
2.축 n에 수직인 벡터 v⟂ = perpn(v) = v - projn(v)
여기서 평행한 벡터 projn(v)은 회전해도변하지 않고, 수직인 부분을 회전하는 방법만 알면 된다.
회전은 Rotate이고 R로 표기하는데 Rn(v) = projn(v) + Rn(v⟂)만 구할 수 있으면 된다.
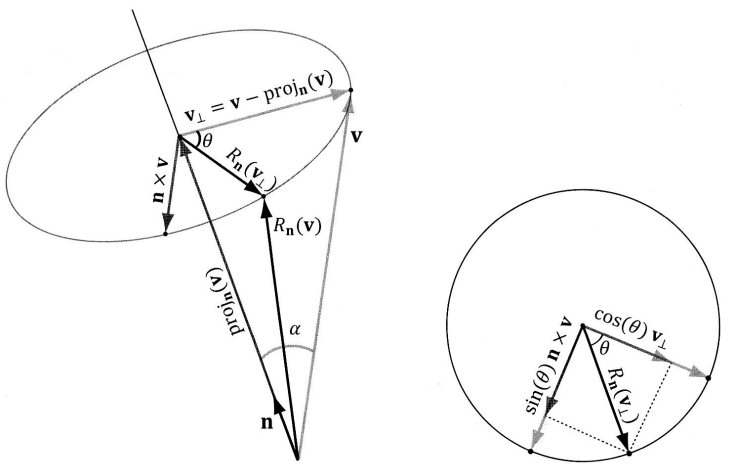
Rn(v⟂)을 먼저 구해보자.
1.v⟂ - projn(v)의 값인 벡터 v⟂를 구한다.
2.외적 n × v을 사용하여 v⟂와 n에 수직인 벡터를 구한다. 왼손 엄지 법칙과 삼각함수 법칙에 따라 값 유도한다.

α는 축 n과 벡터 v 사이의 각도이다. v⟂와 n × v의 크기가 같다. 벡터 두개가 마련되었으니 삼각함수 법칙에 의해 식을 유도할 수 있다.

이제 Rn(v)은 삼각함수에 의해 아래의 일반화 공식을 유도할 수 있다.

유도된 공식을 이용하여 하나의 행렬을 만들면

c는 cosθ이고 s는 sinθ이다. 위의 행렬은 xyz축 회전을 했을 경우이다.
만약 x, y, z축 각각 회전하는 경우를 생각해보자. x 축은 n = (1, 0, 0), y 축은 n = (0, 1, 0), z 축은 n = (0, 0, 1)이 되므로 위 공식에 대입하면 아래와 같은 일반화 공식이 나온다.

'서적 정리 > DirectX11을 이용한 3D 게임 프로그래밍 입문' 카테고리의 다른 글
| 21.변환 행렬 대 좌표 변경 행렬 (0) | 2022.01.20 |
|---|---|
| 20.좌표 변경 변환 (0) | 2022.01.20 |
| 19.변환들의 합성 (0) | 2022.01.20 |
| 18.아핀변환(Affine Transformation) (0) | 2022.01.20 |
| 16.행렬 대수 요약 (0) | 2022.01.20 |
| 15.XNA Math 라이브러리의 행렬 관련 기능 (0) | 2022.01.20 |
| 14.행렬의 역 (0) | 2022.01.20 |
| 13.딸림행렬(Adjoint Matrix) (0) | 2022.01.20 |




댓글