문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/84021
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈 공간에 적절히 올려놓으려 합니다. 게임 보드와 테이블은 모두 각 칸이 1x1 크기인 정사각 격자 모양입니다. 이때, 다음 규칙에 따라 테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈칸에 채우면 됩니다.
- 조각은 한 번에 하나씩 채워 넣습니다.
- 조각을 회전시킬 수 있습니다.
- 조각을 뒤집을 수는 없습니다.
- 게임 보드에 새로 채워 넣은 퍼즐 조각과 인접한 칸이 비어있으면 안 됩니다.
다음은 퍼즐 조각을 채우는 예시입니다.
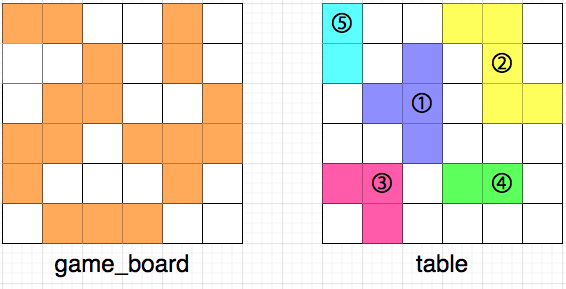
위 그림에서 왼쪽은 현재 게임 보드의 상태를, 오른쪽은 테이블 위에 놓인 퍼즐 조각들을 나타냅니다. 테이블 위에 놓인 퍼즐 조각들 또한 마찬가지로 [상,하,좌,우]로 인접해 붙어있는 경우는 없으며, 흰 칸은 퍼즐이 놓이지 않은 빈 공간을 나타냅니다. 모든 퍼즐 조각은 격자 칸에 딱 맞게 놓여있으며, 격자 칸을 벗어나거나, 걸쳐 있는 등 잘못 놓인 경우는 없습니다.
이때, 아래 그림과 같이 3,4,5번 조각을 격자 칸에 놓으면 규칙에 어긋나므로 불가능한 경우입니다.
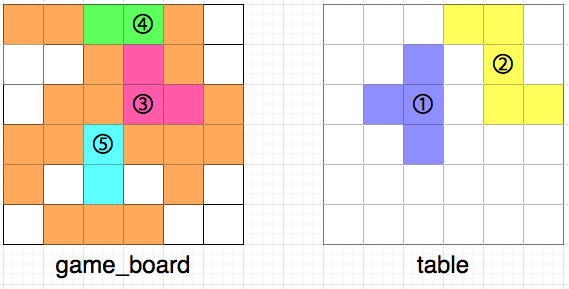
- 3번 조각을 놓고 4번 조각을 놓기 전에 위쪽으로 인접한 칸에 빈칸이 생깁니다.
- 5번 조각의 양 옆으로 인접한 칸에 빈칸이 생깁니다.
다음은 규칙에 맞게 최대한 많은 조각을 게임 보드에 채워 넣은 모습입니다.
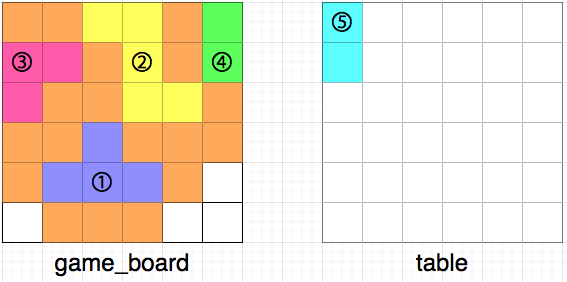
최대한 많은 조각을 채워 넣으면 총 14칸을 채울 수 있습니다.
현재 게임 보드의 상태 game_board, 테이블 위에 놓인 퍼즐 조각의 상태 table이 매개변수로 주어집니다. 규칙에 맞게 최대한 많은 퍼즐 조각을 채워 넣을 경우, 총 몇 칸을 채울 수 있는지 return 하도록 solution 함수를 완성해주세요.
제한사항
- 3 ≤ game_board의 행 길이 ≤ 50
- game_board의 각 열 길이 = game_board의 행 길이
- 즉, 게임 보드는 정사각 격자 모양입니다.
- game_board의 모든 원소는 0 또는 1입니다.
- 0은 빈칸, 1은 이미 채워진 칸을 나타냅니다.
- 퍼즐 조각이 놓일 빈칸은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
- table의 행 길이 = game_board의 행 길이
- table의 각 열 길이 = table의 행 길이
- 즉, 테이블은 game_board와 같은 크기의 정사각 격자 모양입니다.
- table의 모든 원소는 0 또는 1입니다.
- 0은 빈칸, 1은 조각이 놓인 칸을 나타냅니다.
- 퍼즐 조각은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
- game_board에는 반드시 하나 이상의 빈칸이 있습니다.
- table에는 반드시 하나 이상의 블록이 놓여 있습니다.
입출력 예

입출력 예 설명
입출력 예 #1
입력은 다음과 같은 형태이며, 문제의 예시와 같습니다.
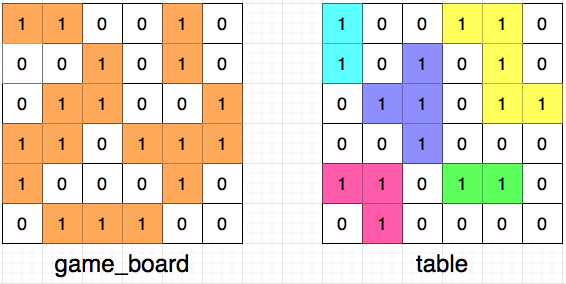
입출력 예 #2
블록의 회전은 가능하지만, 뒤집을 수는 없습니다.
소스 코드
struct Block
{
int x = 0;
int y = 0;
Block( int row, int col )
: x( row ), y( col )
{
}
Block() = default;
bool operator ==( Block rhs )
{
if( rhs.x == x && rhs.y == y )
return true;
return false;
}
bool operator !=( Block rhs )
{
return !( *this == rhs );
}
};
bool CompX( Block a, Block b )
{
return a.x < b.x;
}
bool CompY( Block a, Block b )
{
return a.y < b.y;
}
void MoveToZeroToZeroPoint( vector<vector<Block>>& puzzles )
{
for( int i = 0; i < puzzles.size(); ++i )
{
Block minBlockX = *min_element( puzzles[ i ].begin(), puzzles[ i ].end(), CompX );
Block minBlockY = *min_element( puzzles[ i ].begin(), puzzles[ i ].end(), CompY );
for( int j = 0; j < puzzles[ i ].size(); ++j )
{
puzzles[ i ][ j ].x -= minBlockX.x;
puzzles[ i ][ j ].y -= minBlockY.y;
}
}
}
void Rotate( vector<vector<Block>>& puzzles )
{
for( int i = 0; i < puzzles.size(); ++i )
{
Block maxBlockX = *max_element( puzzles[ i ].begin(), puzzles[ i ].end(), CompX );
Block maxBlockY = *max_element( puzzles[ i ].begin(), puzzles[ i ].end(), CompY );
int size = max( maxBlockX.x, maxBlockY.y ) + 1;
for( int j = 0; j < puzzles[ i ].size(); ++j )
{
Block puzzle = puzzles[ i ][ j ];
puzzles[ i ][ j ].y = puzzle.x;
puzzles[ i ][ j ].x = size - puzzle.y - 1;
}
}
MoveToZeroToZeroPoint( puzzles );
}
void DFS( int row, int col, vector<vector< bool >>& visited, vector<Block>& puzzle, const vector<vector<int>> table, int blank )
{
if( visited[ row ][ col ] == true ) return;
if( table[ row ][ col ] != blank ) return;
visited[ row ][ col ] = true;
puzzle.emplace_back( Block( col, row ) );
int dx[ 4 ] = { 0, 0, -1, +1 };
int dy[ 4 ] = { +1, -1, 0, 0 };
int size = visited.size();
for( int i = 0; i < 4; ++i )
{
int nx = col + dx[ i ];
int ny = row + dy[ i ];
if( nx < 0 || ny < 0 ) continue;
if( nx >= size || ny >= size ) continue;
if( table[ ny ][ nx ] != blank ) continue;
DFS( ny, nx, visited, puzzle, table, blank );
}
}
void Divide( const vector<vector<int>> table, vector<vector<Block>>& puzzles, int blank )
{
int size = table.size();
vector<vector<bool>> visited( size, vector<bool>( size, false ) );
for( int row = 0; row < size; ++row )
{
for( int col = 0; col < size; ++col )
{
if( table[ row ][ col ] != blank ) continue;
if( visited[ row ][ col ] == true ) continue;
vector<Block> puzzle;
DFS( row, col, visited, puzzle, table, blank );
if( puzzle.empty() == false )
puzzles.emplace_back( puzzle );
}
}
}
bool CompareBlock( vector<Block> board, vector<Block> table )
{
int count = 0;
for( int i = 0; i < board.size(); ++i )
{
for( int j = 0; j < table.size(); ++j )
{
if( board[ i ] == table[ j ] )
count++;
}
}
if( count == board.size() )
return true;
return false;
}
void Check( vector<vector<Block>>& board, vector<vector<Block>>& table )
{
for( int i = 0; i < board.size(); ++i )
{
for( int j = 0; j < table.size(); ++j )
{
if( board[ i ].size() != table[ j ].size() )
continue;
if( CompareBlock( board[ i ], table[ j ] ) )
{
board.erase( board.begin() + i );
table.erase( table.begin() + j );
j = -1;
}
}
}
}
int solution( vector<vector<int>> game_board, vector<vector<int>> table )
{
int answer = -1;
vector<vector<Block>> puzzles[ 2 ];
Divide( game_board, puzzles[ 0 ], 0 );
Divide( table, puzzles[ 1 ], 1 );
MoveToZeroToZeroPoint( puzzles[ 0 ] );
MoveToZeroToZeroPoint( puzzles[ 1 ] );
int sum = 0;
for( int i = 0; i < puzzles[ 1 ].size(); ++i )
{
for( int j = 0; j < puzzles[ 1 ][ i ].size(); ++j )
sum++;
}
for( int i = 0; i < 4; ++i )
{
Check( puzzles[ 0 ], puzzles[ 1 ] );
Rotate( puzzles[ 0 ] );
if( puzzles[ 0 ].empty() || puzzles[ 1 ].empty() )
break;
}
int count = 0;
for( int i = 0; i < puzzles[ 1 ].size(); ++i )
{
for( int j = 0; j < puzzles[ 1 ][ i ].size(); ++j )
count++;
}
answer = sum - count;
return answer;
}
생각해 볼 것
문제를 보고 고민을 많이 했다. 이틀 정도 고민하고 내 머리속에 떠오른 방법은 아래와 같다.
- 퍼즐을 조각별로 분해한다.
- 원점을 기준으로 좌표이동 한다.
- 갖고 있는 퍼즐 조각의 칸 수를 저장한다.
- 회전 한 후, 버블 탐색으로 검사한다.
- 일치한 경우 삭제한다.
- 4회전 후 남아 있는 퍼즐 조각의 수와 3에서 저장한 값을 뺀다.
3번 째 입출력 예는 다른 사람이 올린 테스트 케이스다.
'개발 > 프로그래머스' 카테고리의 다른 글
| 동적계획법(Dynamic Programming) > 정수 삼각형 (Level 3) (2) | 2024.11.24 |
|---|---|
| 동적계획법(Dynamic Programming) > N으로 표현 (Level 3) (0) | 2024.11.19 |
| 깊이/너비 우선 탐색(DFS/BFS) > 여행경로 (Level 3) (0) | 2023.03.08 |
| 이분탐색 > 징검다리 (Level 4) (0) | 2022.12.08 |
| 이분탐색 > 입국심사 (Level 3) (0) | 2022.12.08 |
| 깊이/너비 우선 탐색(DFS/BFS) > 게임 맵 최단거리 (Level 2) (0) | 2022.12.08 |
| 탐욕법(Greedy) > 섬 연결하기 (Level 3) (0) | 2022.11.07 |
| 탐욕법(Greedy) > 단속카메라 (Level 3) (0) | 2022.11.05 |




댓글