행렬식은 정방행렬을 받아서 실수 값을 산출하는 함수이다. 정방행렬 A의 행렬식을 흔히 detA로 표기한다.
기하학적으로 행렬식은 부피와 관련이 있는데, 행렬식이 선형변환 하에서 그 부피가 변하는 방식에 대한 정보를 제공함을 증명하는 것이 가능한다. 또한 행렬식은 크라메의 법식(Cramer's rule)을 이용해서 1차 연립방정식을 푸는 데에도 쓰인다.
컴퓨터 그래픽에서 행렬식은 행렬의 역을 구할 때 행렬식이 쓰인다. 행렬의 역을 역행렬이라고 부르고, 역행렬이 존재하기 위해선 정방행렬 A는 오직 detA ≠ 0인 조건이 필요하다.
1.소행렬
n × n 행렬 A가 주어졌을 때, 소행렬 Aij는 A의 i번째 행과 j번째 열을 삭제한 결과로 (n - 1) × (n - 1) 행렬이다.
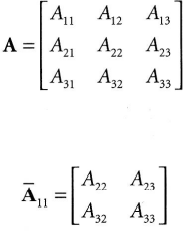
2.행렬식의 정의
한 행렬의 행렬식은 재귀적으로 정의된다. 4 × 4 행렬의 행렬식은 3 × 3 행렬의 행렬식으로 되고, 3 × 3 행렬의 행렬식은 2 × 2 행렬로, 다시 반복하며 1 × 1 행렬이 된다.
행렬 A가 n × n 행렬이고, n > 1일 때 A의 행렬식은 정의할 수 있다.

3차원 그래픽에서는 주로 4 × 4 행렬을 다룬다.
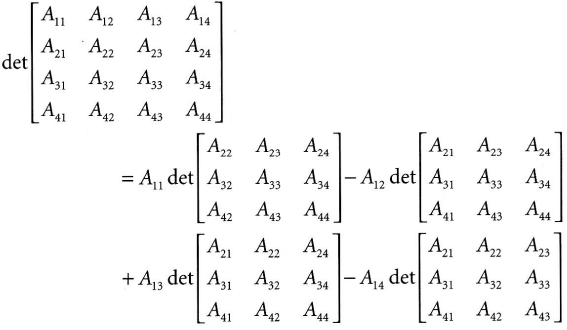
행렬식은 재귀적으로 한다고 했으니, 4 × 4 행렬식으로 인해 만들어진 3 × 3 행렬의 행렬식은 다시 2 × 2 행렬로 반복할 것이다.
사실 말이 1 × 1 행렬까지 반복이지 3 × 3 행렬까지만 구하면 된다.
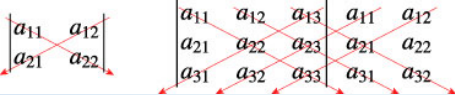
우하양 화살표인 경우 +, 좌하양 화살표인 경우-로 하면된다.
2 × 2 행렬의 경우 a11a22 - a12a21이다.
3 × 3 행렬의 경우 a11a22a33 + a12a23a31 + a13a21a32 -(a13a22a31 + a11a23a32 + a12a21a33)이다.

위의 행렬을 M이라고 할 때, detM은 3(7) - 4(3)이 될 것이고, 결과는 21 - 12 = 9이므로 detM = 9가 된다.
'서적 정리 > DirectX11을 이용한 3D 게임 프로그래밍 입문' 카테고리의 다른 글
| 16.행렬 대수 요약 (0) | 2022.01.20 |
|---|---|
| 15.XNA Math 라이브러리의 행렬 관련 기능 (0) | 2022.01.20 |
| 14.행렬의 역 (0) | 2022.01.20 |
| 13.딸림행렬(Adjoint Matrix) (0) | 2022.01.20 |
| 11.단위행렬(Identity Matrix) (0) | 2022.01.20 |
| 10.행렬의 전치 (0) | 2022.01.20 |
| 9.행렬 곱셈 (0) | 2022.01.20 |
| 8.행렬 정의 (0) | 2022.01.20 |




댓글