한 좌표계의 좌표를 다른 좌표계의 좌표로 변환하는 것을 좌표 변경 변환(change of coordinate transformation)이라고 한다.

위 그림을 보면 벡터 v는 변하지 않았음에도 좌표계 A와 B에 따라서 위치가 달라지는 것을 볼 수 있다. 즉, 좌표계가 변함으로써 기하구조적의 좌표 표현도 따라서 변하게 된다.
3차원 컴퓨터 그래픽에서 여러 개의 좌표계를 사용하는 경우가 많고, 위치는 벡터가 아니라 점의 속성이기 때문에, 점에 대한 좌표계 변환과 벡터에 대한 좌표계 변환은 다르다.
1.벡터
좌표계 A와 B, 벡터 p가 있을 때, 좌표계 A를 기준으로 한 벡터 p의 좌표가 PA = (x, y)이라고 한다면, 좌표계 B의 PB = (x', y')는 어떻게 구해야 할까?

좌표계 B를 보면 u와 v는 좌표계 A의 x축, y축의 단위벡터이다. 따라서 xu는 PA의 x좌표이고, yv는 PA의 y좌표이다.
좀 더 나아가 u = (1, 0)이고, v = (0, 1)이므로 PA = xu + yv로 표현할 수있다. 좌표계 B 역시 마찬가지 방식으로 표현할 수 있다.

결론적으로, 만일 PA = (x, y)가 주어졌고 벡터 uB = (ux, uy)와 vB = (vx, vy)를 안다면 PB = (x', y')를 구할 수 있다.
3차원 역시 비슷하다. 3차원으로 일반화하면

u, v, w는 각각 좌표게 A의 x, y, z 축 방향 단위벡터이다.
2.점
점의 경우 위치가 중요하므로 벡터를 이동시키는 방식으로 점을 이동할 수 없다.

위 그림에서 주의해서봐야할 것은 벡터와 다르게 점 P이 좌표계 A에서 B로 변환한다고 해서 바뀌지 않는다는 점이다. 벡터는 상대적인 느낌이였다면 점은 절대적이라고 생각하면 될 것 같다.
좌표계 A를 보면 u와 v는 각각 x축, y축의 단위벡터이고 Q는 좌표계 B의 원점에서 부터 좌표계 A의 원점까지의 벡터이다. 따라서 PA = (x, y)는 PA = xu + yv로 표현할 수 있다. 점 P를 좌표계 B로 변환한다면 아래와 같이 표현할 수 있다.

결론적으로, 만일 PA = (x, y)가 주어졌고 벡터 ub = (ux, uy)와 vb = (vx, vy), Qb = (Qx, Qy)를 안다면 PB = (x', y')를 구할 수 있다.
3차원 역시 비슷하다. 3차원으로 일반화하면
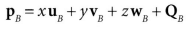
u, v, w는 각각 좌표게 A의 x, y, z 축 방향 단위벡터고 Q는 A의 원점이다.
3.행렬 표현
벡터와 점에 대한 좌표 변경 변환을 정리해보자.
벡터의 경우 : (x', y', z') = xuB + yvB + zwB
점의 경우 : (x', y', z') = xuB + yvB + zwB + QB
동차좌표를 사용한다면 벡터와 점을 하나의 공식으로 처리할 수 있다.

w = 0이면 벡터에 대한 좌표 변경 변환을 의미하게 되고, w = 1이면 점에 대한 좌표 변경 변환을 의미하게 된다.
즉, w 좌표를 제대로 설정만 하면 벡터와 점 모두에 적용할 수 있다. 따라서 개별적인 두 개의 공식을 둘 필요가 없다. 하나로 통합한 공식을 행렬료 표현해보자.

여기서 QB = (Qx, Qy, Qz, 1), uB = (ux, uy, uz, 0), vB = (vx, vy, vz, 0), wB = (wx, wy, wz, 0)은 좌표계 A의 원점(QB)과 축들(uB, vB, wB)의 좌표계 B 기준 동차좌표들이다. A 기준 좌표들을 B 기준 좌표들로 변환사상하는 식 4 × 4행렬을 좌표 변경 행렬 혹은 좌표계 변환 행렬, 좌표변환 행렬이라고 부른다.
4.결합법칙과 좌표 변경 행렬
세 개의 좌표계 F, G, H가 있고, A가 F에서 G로의 좌표계 변환 행렬이고 B가 G에서 H로의 좌표계 변환 행렬이라고 하자.
보기 편하게 표현해보면
A : F -> G
B : G -> H
어떤 벡터의 F기준 좌표 pF를 H 기준 좌표 pH로 변환(F -> H)하려면 좌표계 F에서 G로 변환하고 H로 변환하는 방법이 있을 것이다.
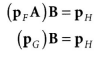
행렬의 곱셉은 결합법칙을 만족하므로, 좀 더 간단하게 표현할 수 있다.

행렬곱 AB은 F에서 H로 가는 좌표계 변환 행렬이다. 즉, AB의 행렬을 미리 갖고 있는다면 좌표계 F에서 H로의 변환을 행렬 한번의 곱으로 처리할 수 있다.
5.역행렬과 좌표 변경 행렬
좌표계 B의 벡터 p를 Pb라고 하고, M이 좌표계 A에서 B로의 좌표 변경 행렬이라고 하자(A -> B).
이를 식으로 나타내면 pB= pAM으로 표현할 수 있다. M이 가역행렬이라면 역행렬이 존재한다. 좌표계 B에서 A로의 좌표 변경 행렬은 M의 역행렬을 사용하여 pBM-1 = pA로 변환할 수 있다.

결론적으로 좌표계 A에서 다른 좌표계 B로의 좌표 변경 행렬을 알고 있고, 이 좌표 변경 행렬의 역행렬이 존재한다면, 다른 좌표계 B에서 기존 좌표계 A로의 변환도 가능하다. 쉽게 말해서 롤백이 가능하다.

'서적 정리 > DirectX11을 이용한 3D 게임 프로그래밍 입문' 카테고리의 다른 글
| 24.Direct3D 기본지식 (0) | 2022.01.20 |
|---|---|
| 23.변환 요약 (0) | 2022.01.20 |
| 22.XNA Math 라이브러리의 관련 함수들 (0) | 2022.01.20 |
| 21.변환 행렬 대 좌표 변경 행렬 (0) | 2022.01.20 |
| 19.변환들의 합성 (0) | 2022.01.20 |
| 18.아핀변환(Affine Transformation) (0) | 2022.01.20 |
| 17.선형변환 (0) | 2022.01.20 |
| 16.행렬 대수 요약 (0) | 2022.01.20 |




댓글